Unlocking The Mystery: What "A Cube Has 12 Of Them" Truly Means
The phrase "a cube has 12 of them" might sound like a riddle, a simple mathematical fact, or even a line from a children's book, but for many, it immediately brings to mind the challenge and satisfaction of solving a crossword puzzle. This seemingly straightforward statement holds a deeper significance, not just in the realm of puzzles but also in the fundamental understanding of geometry and the structures that define our physical world. It's a classic clue that has graced countless grids, from the quick daily challenges to more intricate weekend editions, consistently pointing to one specific, foundational element of a cube.
Beyond its common appearance in word games, this particular characteristic of a cube—the fact that it possesses exactly twelve of a certain feature—is central to its definition and its practical applications across various fields. Understanding what these "them" are is not just about getting the right answer in a puzzle; it's about grasping the very essence of three-dimensional shapes, their properties, and how they interact with the space around us. Let's delve into the world of cubes, crosswords, and the crucial elements that make this geometric marvel what it is.
Table of Contents
- The Enduring Mystery of "A Cube Has 12 of Them": Crossword Unraveled
- Deconstructing the Cube: A Geometric Marvel
- The Ubiquitous Nature of Edges in Our World
- From Ancient Geometry to Modern Design: The Role of Edges
- The Psychology Behind Solving "A Cube Has 12 of Them"
- Beyond the Basics: Advanced Concepts of Edges
- Practical Applications and Real-World Significance
- Expert Insights: Why Understanding Edges Matters
The Enduring Mystery of "A Cube Has 12 of Them": Crossword Unraveled
For avid crossword solvers, the clue "a cube has 12 of them" is as familiar as the morning coffee. It’s a staple, a go-to, and often one of the first clues newcomers learn to recognize. Its frequent appearance in puzzles like the NYT Mini, the Daily Themed Crossword, and various other major publications speaks to its elegant simplicity and its foundational truth. This clue, typically requiring a five-letter answer, is a perfect example of how crosswords blend general knowledge with logical deduction, making it accessible yet satisfying.
The beauty of such a clue lies in its directness. It doesn't rely on obscure trivia or complex wordplay. Instead, it taps into basic geometric understanding that most people acquire in their early education. Yet, in the pressure of a timed puzzle or when faced with a blank grid, even the simplest facts can momentarily escape us. This is where the thrill of the solve comes in, that "aha!" moment when the correct term clicks into place, revealing the structure of the cube.
Unraveling the Crossword Clue: "Edges" Revealed
The answer, of course, is "EDGES." This five-letter word perfectly fits the bill and is consistently confirmed across numerous crossword databases and puzzle solutions. Whether you encountered it in the NYT Mini on September 11, 2024, or the Daily Themed Crossword on December 25, 2021, the solution remains the same. The consistency of this answer across different puzzles and dates (like December 18, 2024, for the NYT) underscores its status as a fundamental geometric property and a beloved crossword staple.
An edge of a cube is a line segment where two faces meet. Imagine a standard six-sided die. Each straight line that forms the boundary of a face, and where two faces join, is an edge. If you count them, you will indeed find exactly twelve of them. This simple count is the key to unlocking the clue. The clue's elegance lies in its ability to prompt a mental visualization of a cube and a quick enumeration of its defining linear components.
Why Crosswords Love Geometric Clues
Crossword constructors frequently turn to geometry for clues because geometric properties are universal, unchanging, and often quantifiable. Unlike historical facts that might be debated or cultural references that can become dated, the properties of shapes like "a cube has 12 of them" remain constant. This makes them reliable and fair game for puzzles aimed at a broad audience. They test fundamental knowledge rather than niche expertise, providing a sense of accomplishment for solvers of all levels.
Moreover, geometric clues often lend themselves to concise, elegant phrasing. "A cube has 12 of them" is short, precise, and directly leads to the answer without needing convoluted hints. This efficiency is highly valued in crossword construction, where every letter and word counts. Such clues serve as anchor points in the grid, helping solvers gain traction and fill in surrounding letters, which then aids in solving more complex or obscure clues.
Deconstructing the Cube: A Geometric Marvel
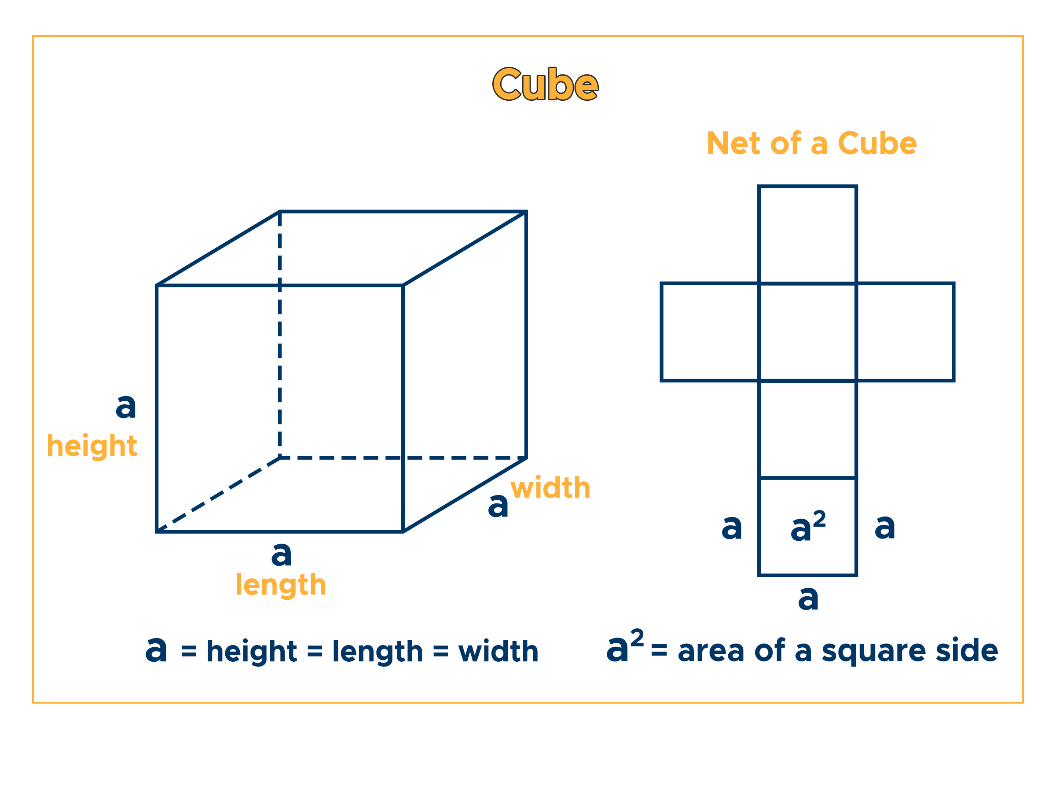
The cube, also known as a regular hexahedron, is one of the five Platonic solids, a set of convex regular polyhedra. Its perfect symmetry and predictable properties make it a cornerstone of geometry and a foundational shape in understanding three-dimensional space. To truly appreciate what "a cube has 12 of them" refers to, we must first understand the cube's fundamental components.
A cube is defined by three primary elements: faces, vertices, and edges. Each plays a crucial role in giving the cube its distinct shape and characteristics. While the clue specifically asks about one of these, understanding all three provides a holistic view of this fascinating geometric figure. The interplay between these elements is what makes the cube such a stable and versatile shape, appearing everywhere from dice to building blocks, and from crystal structures to computer graphics.
Faces, Vertices, and the Elusive Edges
Let's break down the components of a cube:
- Faces: These are the flat surfaces that form the boundary of the cube. A cube has 6 faces, and each face is a perfect square. Think of the six sides of a standard die. These faces are congruent, meaning they are identical in shape and size, contributing to the cube's overall symmetry.
- Vertices: These are the points where three or more edges meet. A cube has 8 vertices. Imagine the corners of a box; each corner is a vertex. These points define the extreme boundaries of the cube, acting as the structural anchors for its edges and faces.
- Edges: As we've established, these are the line segments where two faces meet. A cube has 12 edges. Each edge is a straight line, and all edges of a cube are of equal length. This equal length is what makes the cube a "regular" polyhedron, ensuring its perfect symmetry and consistent dimensions. It's these 12 distinct linear boundaries that form the framework of the cube, giving it its rigid structure.
The relationship between these components is often described by Euler's formula for polyhedra: V - E + F = 2, where V is the number of vertices, E is the number of edges, and F is the number of faces. For a cube, this holds true: 8 (vertices) - 12 (edges) + 6 (faces) = 2. This formula underscores the fundamental mathematical consistency of polyhedra and confirms the count of 12 edges as an intrinsic property of a cube.
The Ubiquitous Nature of Edges in Our World
While the crossword clue focuses on "a cube has 12 of them" in a purely geometric sense, the concept of edges extends far beyond the mathematical definition. Edges are fundamental to how we perceive and interact with the physical world. Every object around us, from the screen you're reading this on to the table it rests upon, is defined by its edges. They mark boundaries, define forms, and dictate how light interacts with surfaces.
In architecture, edges define the lines of buildings, creating a sense of structure and form. In nature, crystal formations exhibit precise edges, reflecting their underlying atomic structures. Even in abstract art, edges can be used to create tension, movement, and visual interest. The human eye is naturally drawn to edges as they provide critical information about an object's shape, depth, and orientation in space. Without edges, objects would appear as amorphous blobs, indistinguishable from one another.
Consider the practical implications: the sharpness of a knife's edge, the protective edge of a curb, or the leading edge of an airplane wing. In each case, the edge plays a critical functional role. It's not just a theoretical line but a tangible feature with real-world consequences, whether for cutting, guiding, or creating aerodynamic lift. The very concept of "cutting-edge" technology implies being at the forefront, pushing boundaries—much like an edge defines the boundary of a shape.
From Ancient Geometry to Modern Design: The Role of Edges
The study of edges, vertices, and faces dates back to ancient civilizations. Greek mathematicians like Euclid meticulously documented the properties of geometric shapes, including the cube, laying the groundwork for all subsequent geometry. Their observations on what "a cube has 12 of them" formed part of a comprehensive understanding of spatial relationships that was crucial for architecture, navigation, and astronomy.
In modern design and engineering, the precise understanding of edges is paramount. From the clean lines of minimalist furniture to the intricate networks of microchips, edges dictate functionality and aesthetics. Industrial designers carefully craft edges to ensure ergonomic comfort and visual appeal. Engineers consider the strength and stress points along edges when designing structures, ensuring safety and durability. The concept of "edge cases" in software development refers to the extreme boundaries of a system's functionality, highlighting how the idea of a boundary or limit, much like a geometric edge, is crucial in problem-solving.
Even in the digital realm, edges are fundamental. Computer graphics rely on polygons (which are defined by their edges) to render realistic 3D models. The crispness of an image, the detail in a rendered scene, all depend on how effectively edges are defined and processed. This continuity from ancient philosophical inquiry to cutting-edge technological application demonstrates the enduring relevance of these basic geometric principles.
The Psychology Behind Solving "A Cube Has 12 of Them"
The satisfaction derived from solving a crossword clue like "a cube has 12 of them" goes beyond simply knowing the answer. It taps into cognitive processes that are beneficial for mental acuity. Crossword puzzles, in general, are known to improve vocabulary, critical thinking, and memory. This particular clue, while seemingly simple, engages several cognitive functions:
- Visualization: Solvers must mentally conjure an image of a cube.
- Recall: They need to access their stored knowledge about the properties of geometric shapes.
- Counting/Enumeration: A quick mental count of the edges confirms the answer.
- Pattern Recognition: Experienced solvers recognize the common phrasing of such geometric clues.
The "aha!" moment when the answer "edges" comes to mind is a burst of dopamine, a reward for the brain for making a successful connection. This positive reinforcement encourages continued engagement with puzzles, contributing to sustained cognitive health. It's a testament to how seemingly trivial puzzles can offer significant mental benefits, keeping our brains sharp and agile. The process of searching for answers, even for a well-known clue like "a cube has 12 of them," exercises the neural pathways involved in problem-solving and information retrieval.
Beyond the Basics: Advanced Concepts of Edges
While the simple count of 12 edges satisfies the crossword clue, the concept of an edge extends into more complex mathematical and scientific domains. In graph theory, for instance, a graph is composed of vertices (nodes) and edges (connections between nodes). This abstract representation is used to model networks of all kinds, from social networks to computer networks, where edges represent relationships or pathways.
In topology, which studies properties of spaces that are preserved under continuous deformations, edges are crucial for defining the boundaries of surfaces and volumes. The concept of an "orientable edge" is vital in understanding how surfaces can be "stitched" together. In computational geometry, algorithms are developed to detect, classify, and manipulate edges in 3D models, which is fundamental for tasks like object recognition, robotic navigation, and virtual reality.
Furthermore, in materials science, the "edges" of crystal grains can significantly impact a material's properties, such as its strength and conductivity. Defects or impurities often accumulate at these grain boundaries (edges), influencing how the material behaves under stress. This demonstrates how a seemingly simple geometric concept scales up to explain complex phenomena at the microscopic level, highlighting the depth of understanding required in specialized fields.
Practical Applications and Real-World Significance
The knowledge that "a cube has 12 of them" and what those "them" are (edges) isn't just for puzzle enthusiasts. This fundamental geometric understanding has profound practical applications across numerous industries and scientific disciplines. From the design of everyday objects to advanced scientific research, edges play a critical role.
In manufacturing, the precision of edges is paramount. Whether it's cutting steel beams for a skyscraper or fabricating microscopic components for electronics, the accuracy of the edges determines the quality and functionality of the final product. Architects rely on the defined edges of structural elements to ensure stability and aesthetic appeal in buildings. Urban planners consider the edges of parks, roads, and neighborhoods to define boundaries and facilitate navigation.
Even in fields like biology, the concept of edges is relevant. The boundaries of cells, the folds of proteins, or the branching patterns of neural networks can be analyzed in terms of their edges, providing insights into their structure and function. This ubiquitous presence underscores why understanding basic geometric properties, like those of a cube, is more than just academic; it's a foundational skill for interacting with and shaping our world.
Edges in Computer Graphics and 3D Modeling
One of the most visually impactful applications of edges is in computer graphics and 3D modeling. When artists and designers create virtual worlds, characters, or objects, they essentially build them from a mesh of vertices and edges. These edges form the wireframe skeleton of any 3D model. The more edges a model has, the more detailed and smooth it can appear when rendered.
Techniques like edge detection are crucial in image processing, allowing computers to identify the boundaries of objects within an image. This is vital for facial recognition, autonomous driving, and medical imaging. In animation, the manipulation of edges allows for the deformation of characters and objects, bringing them to life. The ability to precisely control and render "a cube has 12 of them" in a digital environment is what makes virtual reality immersive, video games realistic, and animated films breathtaking.
Expert Insights: Why Understanding Edges Matters
From an expert perspective, understanding the properties of shapes like the cube, particularly its edges, is not just about rote memorization but about grasping fundamental principles of spatial reasoning. This foundational knowledge underpins numerous advanced fields:
- Mathematics: It's the basis for topology, graph theory, and differential geometry.
- Engineering: Crucial for structural analysis, material science, and mechanical design.
- Computer Science: Essential for computer vision, robotics, and 3D graphics.
- Architecture and Design: Fundamental for creating stable, functional, and aesthetically pleasing structures.
The simplicity of "a cube has 12 of them" belies its profound importance. It's a gateway to understanding complex systems and designing innovative solutions. Experts in these fields leverage this basic knowledge daily, whether they are optimizing the flow of data through a network (graph theory), ensuring the structural integrity of a bridge (engineering), or rendering a hyper-realistic scene in a video game (computer graphics). The ability to visualize and manipulate these fundamental components of geometry is a hallmark of expertise in many STEM disciplines.
Conclusion
What began as a simple crossword clue, "a cube has 12 of them," reveals itself to be a powerful entry point into the fascinating world of geometry, problem-solving, and real-world application. The answer, "edges," is far more than just a five-letter solution; it represents a fundamental component of one of the most perfect and ubiquitous shapes in existence. From the satisfying click of a solved puzzle to the intricate designs of modern technology, the concept of edges is an indispensable part of our understanding and manipulation of the three-dimensional world.
We've explored how this clue functions in crosswords, delved into the geometric definition of a cube's edges, and examined their pervasive presence and importance in everything from ancient mathematics to cutting-edge computer graphics. So, the next time you encounter "a cube has 12 of them" in a puzzle, remember that you're not just solving a clue; you're engaging with a piece of universal knowledge that connects us to millennia of human ingenuity and observation. What other seemingly simple facts hold such profound depth? Share your thoughts in the comments below, or explore more of our articles on the intriguing connections between everyday knowledge and deeper scientific principles!

A cube has 12 edges 6 faces and 8 vertices | StudyX

Cube Numbers Explained | A PlanBee Blog
Cubic Shape